Методическое письмо о проведении государственной итоговой аттестации по образовательным программам основного общего и среднего общего образования по математике в форме государственного выпускного экзамена (письменная и устная формы)
Москва, 2015
Оглавление
Перечень условных обозначений, сокращений и терминов. 3
1. Проведение ГИА-9 по математике в форме ГВЭ (письменная и устная формы) 4
1.1. Особенности экзаменационной работы ГВЭ-9 по математике (письменная форма) 4
1.1.1. Оценивание результатов экзамена ГВЭ-9 по математике (письменная форма) ……………………………………………………………………………….10
1.2. Особенности экзаменационной работы ГВЭ-9 по математике (устная форма) 11
Оценка выполнения отдельных заданий экзаменационной работы и оценивание результатов экзамена. 15
Критерии оценки выполнения отдельных заданий экзаменационной работы.. 15
2. Проведение ГИА-11 по математике в форме ГВЭ (письменная и устная формы) 17
2.1. Особенности экзаменационной работы ГВЭ-11 по математике (письменная форма) 17
2.1.1. Оценивание результатов экзамена ГВЭ-11 по математике (письменная форма) 24
2.2. Особенности экзаменационной работы ГВЭ-11 по математике (устная форма) 25
Оценка выполнения отдельных заданий экзаменационной работы и оценивание результатов экзамена. 28
Критерии оценки выполнения отдельных заданий экзаменационной работы.. 29
Приложение 1. Справочные материалы по математике для участников ГВЭ-9. 31
Приложение 2. Справочные материалы по математике для участников ГВЭ-11. .34
Перечень условных обозначений, сокращений и терминов
|
ГВЭ |
Государственный выпускной экзамен |
|
ГИА |
Государственная итоговая аттестация по образовательным программам основного общего и среднего общего образования |
|
ГИА-11 |
Государственная итоговая аттестация по образовательным программам среднего общего образования |
|
ГИА-9 |
Государственная итоговая аттестация по образовательным программам основного общего образования |
|
ГЭК |
Государственная экзаменационная комиссия субъекта Российской Федерации |
|
Минобрнауки России |
Министерство образования и науки Российской Федерации |
|
Обучающиеся с ОВЗ |
Обучающиеся по образовательным программам основного общего и среднего общего образования с ограниченными возможностями здоровья |
|
ОГЭ |
Основной государственный экзамен |
|
Порядок ГИА-11 |
Приказ Минобрнауки России от 26.12.2013 № 1400 «Об утверждении Порядка проведения государственной итоговой аттестации по образовательным программам среднего общего образования» (зарегистрирован Минюстом России 03.02.2014, регистрационный № 31205) (в редакции приказа Минобрнауки России от 16.01.2015 № 9 (зарегистрирован Минюстом России 30.01.2015, регистрационный № 35794); |
|
Порядок ГИА-9 |
Приказ Минобрнауки России от 25.12.2013 № 1394 «Об утверждении Порядка проведения государственной итоговой аттестации по образовательным программам основного общего образования» (зарегистрирован Минюстом России 03.02.2014, регистрационный № 31206) (в редакции приказа Минобрнауки России от 16.01.2015 № 10 (зарегистрирован Минюстом России 27.01.2015, регистрационный № 35731) |
|
ППЭ |
Пункт проведения экзамена |
|
РЦОИ |
Региональный центр обработки информации субъекта Российской Федерации |
|
СКОО |
Специальная (коррекционная) образовательная организация |
|
ЭМ |
Экзаменационные материалы |
В данном Методическом письме даются разъяснения по вопросам ЭМ для ГВЭ для обучающихся, освоивших образовательные программы основного общего образования и среднего общего образования по математике (письменная и устная формы).
В письме комментируются подходы к отбору содержания экзаменационных материалов, описываются экзаменационные модели и типы заданий, формулируются требования по организации и проведению экзамена, даются рекомендации по оцениванию экзаменационных работ участников экзамена, приводятся образцы заданий.
ГВЭ для обучающихся, освоивших образовательные программы основного общего образования (далее – ГВЭ-9), проводится в соответствии с Порядком ГИА-9.
Категории обучающихся, сдающих ГИА в форме ГВЭ, перечислены в пункте 7. Порядка ГИА-9.
ЭМ соответствуют Федеральному компоненту государственного стандарта общего образования (Приказ Минобразования России от 05.03.2004 г. № 1089).
1.1. Особенности экзаменационной работы ГВЭ-9 по математике (письменная форма)
При разработке экзаменационной модели соблюдалась преемственность с традиционными и новыми формами экзамена по математике для обучающихся, освоивших образовательные программы основного общего образования.
На экзамене проверяется сформированность представлений выпускников о математике как универсальном языке науки, об идеях и методах математики, овладение математическими знаниями и умениями, соответствующими Федеральному компоненту государственного стандарта общего образования (Приказ Минобразования России от 05.03.2004 г. №1089), развитие логического мышления, пространственного воображения, алгоритмической культуры.
Для проведения ГВЭ-9 по математике разработаны варианты экзаменационных работ, включающие в себя задания как по курсу «Алгебра», так и по курсу «Геометрия» (см. образец экзаменационной работы по математике для проведения ГВЭ-9). Эти работы предназначены и для тех выпускников, которые осваивали программу в рамках двух предметов, и для тех, кто изучал математику в рамках интегрированного курса.
На выполнение экзаменационной работы по математике даётся 3 часа 55 минут (235 минут).
В указанном Порядке ГИА-9 формулируются следующие требования проведения экзамена:
«В продолжительность экзаменов по учебным предметам не включается время, выделенное на подготовительные мероприятия (инструктаж обучающихся, вскрытие пакетов с экзаменационными материалами, заполнение регистрационных полей экзаменационной работы, настройка технических средств).
При продолжительности экзамена 4 и более часа организуется питание обучающихся.
Для обучающихся с ОВЗ, обучающихся детей-инвалидов и инвалидов, а также тех, кто обучался по состоянию здоровья на дому, в образовательных организациях, в том числе санаторно-курортных, в которых проводятся необходимые лечебные, реабилитационные и оздоровительные мероприятия для нуждающихся в длительном лечении, продолжительность экзамена увеличивается на 1,5 часа.»
При проведении экзамена для участников с ограниченными возможностями здоровья присутствуют ассистенты, оказывающие экзаменуемым необходимую техническую помощь с учетом их индивидуальных возможностей: помощь в занятии рабочего места, передвижении, сурдопереводе (см. п. 34 и 37 Порядка ГИА-9).
Экзаменационный вариант (маркирован буквой «А») включает 10 заданий: одно задание по арифметике, одно задание по теории вероятностей, семь заданий по алгебре, одно задание по геометрии. Задания являются стандартными для курса математики основной школы. Все они, кроме одного, относятся к заданиям с развернутым ответом и требуют записи решения задачи, демонстрирующей умение выпускника математически грамотно излагать решение, приводя при этом необходимые пояснения и обоснования. При выполнении задания 4 (или аналогичного ему) достаточно дать краткий ответ на каждый из поставленных вопросов.
Структура работы отвечает задаче построения системы дифференцированного обучения в современной школе. Дифференциация обучения направлена на достижение двух целей: формирования у всех учащихся базовой математической подготовки, составляющей функциональную основу общего образования; одновременного создания для части школьников условий, способствующих получению подготовки повышенного уровня, достаточной для активного использования математики в дальнейшем обучении.
Задания в экзаменационном варианте расположены по нарастанию сложности. Задания 1-7 соответствуют уровню базовой математической подготовки, задания 8-10 – уровню повышенной подготовки.
В своей совокупности варианты охватывают все блоки содержания, традиционно представленные в курсе математики 5-9-х классов, что обеспечивает достаточную полноту проверки овладения содержанием курса. В соответствии со спецификой курса математики основное внимание уделяется проверке практической составляющей математической подготовки выпускников, когда овладение теоретическими положениями проверяется опосредованно через проверку умения решать задачи. Все задания, используемые для составления экзаменационных вариантов, содержатся в открытом банке заданий ОГЭ.
Вместе с экзаменационным вариантом участникам экзамена выдаются справочные материалы, содержащие таблицу квадратов двузначных чисел, основные формулы по алгебре и геометрии (см. Приложение 1). При выполнении экзаменационной работы допускается использование линейки, использование калькулятора не разрешается.
При проверке математической подготовки выпускников оценивается уровень, на котором сформированы следующие умения:
выполнять арифметические действия, сочетая устные и письменные приемы;
проводить по известным формулам и правилам преобразования буквенных выражений;
вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования;
читать графики элементарных функций;
решать линейные и квадратные уравнения и неравенства, их системы;
моделировать реальные ситуации на языке теории вероятностей и статистики, вычислять в простейших случаях вероятности событий;
решать планиметрические задачи на нахождение геометрических величин (длин, углов, площадей);
проводить доказательные рассуждения в ходе решения задач.
В 2015 г. для государственной итоговой аттестации выпускников, освоивших образовательные программы основного общего образования в специальных (коррекционных) образовательных организациях для обучающихся с ОВЗ, разработаны специальные ЭМ по математике для проведения ГВЭ-9.
Экзаменационный вариант (маркирован буквой «К») включает 10 заданий: два задания по арифметике, два задания по теории вероятностей и статистике, пять заданий по алгебре, одно задание по геометрии. Образец варианта соответствующей экзаменационной работы приводится ниже. В данной работе все задания относятся к уровню базовой подготовки.
При проверке математической подготовки выпускников, освоивших образовательные программы основного общего образования в специальных (коррекционных) образовательных организациях для обучающихся с ограниченными возможностями здоровья, оценивается уровень, на котором сформированы следующие умения:
выполнять арифметические действия, сочетая устные и письменные приемы;
проводить по известным формулам и правилам преобразования буквенных выражений;
вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования;
читать графики элементарных функций;
решать линейные и квадратные уравнения;
моделировать реальные ситуации на языке теории вероятностей, вычислять в простейших случаях вероятности событий;
решать планиметрические задачи на нахождение геометрических величин (длин, углов, площадей);
извлекать информацию из таблиц и диаграмм, преобразовывать ее с целью ответа на вопрос задачи;
располагать числа на координатной прямой.
Ниже приведены образцы экзаменационных работ для проведения ГВЭ-9 по математике.
Следует иметь в виду, что образцы предназначены для того, чтобы дать возможность составить представление о структуре будущей экзаменационной работы, числе, форме и уровне сложности заданий, и не отражает всех элементов содержания, которые будут проверяться с помощью вариантов экзаменационной работы.
Образец (А) экзаменационного варианта для проведения ГВЭ-9 по математике
Часть 1
1. Решите уравнение:  .
.
2. Упростите выражение:  .
.
3. Решите систему неравенств:  .
.
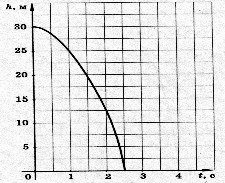
4. Мяч упал с балкона на землю. График на рисунке показывает, как во время падения менялась высота мяча над землей.
|
Используя график, ответьте на вопросы:
а) С какой высоты упал мяч?
б) Сколько времени падал мяч?
в) Какое расстояние пролетел мяч за первую секунду? |
|
5. На экзамене 20 билетов, Сергей не выучил 3 из них. Найдите вероятность того, что ему попадётся выученный билет.
6. Товар на распродаже уценили на 30%, при этом он стал стоить 700 р. Сколько рублей стоил товар до распродажи?
7. Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные  и
и  соответственно.
соответственно.

Часть 2
8. Расположите числа в порядке возрастания:  ;
;  и
и  .
.
9. Решите уравнение:  .
.
10. Один из катетов прямоугольного треугольника на 2 см больше другого, а его площадь меньше 60 см2. Какую длину может иметь больший катет?
Образец (К) экзаменационного варианта для проведения ГВЭ-9 по математике (для обучающихся с ОВЗ)
1. Решите уравнение:  .
.
2. Упростите выражение:  .
.
3. Вычислите:  .
.
4. Одно из чисел  ,
,  ,
,  ,
,  отмечено на числовой прямой, изображенной на рисунке, точкой A. Какое это число?
отмечено на числовой прямой, изображенной на рисунке, точкой A. Какое это число?

5. Найдите значение выражения  .
.
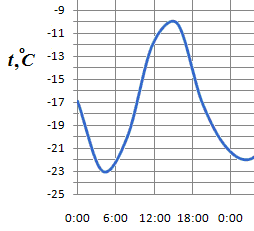
6. График, изображенный на рисунке, показывает, как менялась в течение суток температура воздуха. По горизонтали указывается время суток, по вертикали — значение температуры в градусах Цельсия. Какова была наибольшая температура в течение этих суток?
7. В лыжных гонках участвуют 11 спортсменов из России, 6 спортсменов из Норвегии и 3 спортсмена из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен из Норвегии.
8. Кофейник, который стоил 900 рублей, продаётся с 10-процентной скидкой. Сколько стоит кофейник со скидкой?
9. Студент Петров выезжает из Наро-Фоминска в Москву на занятия в университет. Занятия начинаются в 9:00. В таблице приведено расписание утренних электропоездов от станции Нара до Киевского вокзала в Москве в некотором интервале времени.
|
Отправление от ст. Нара |
Прибытие на Киевский вокзал |
|
6:35 |
7:59 |
|
7:05 |
8:15 |
|
7:28 |
8:30 |
|
7:34 |
8:57 |
Путь от вокзала до университета занимает 40 минут. Укажите время отправления от станции Нара самого позднего из электропоездов, которые подходят студенту.
10. Найдите угол  равнобедренной трапеции
равнобедренной трапеции  , если диагональ
, если диагональ  образует с основанием
образует с основанием  и боковой стороной
и боковой стороной  углы, равные
углы, равные  и
и  соответственно.
соответственно.

1.1.1. Оценивание результатов экзамена ГВЭ-9 по математике (письменная форма)
В Порядке ГИА-9 определены следующие подходы к оценке экзаменационных работ в форме ГВЭ-9:
«Экзаменационные работы проверяются двумя экспертами. По результатам проверки эксперты независимо друг от друга выставляют баллы за каждый ответ на задания экзаменационной работы. Результаты каждого оценивания вносятся в протоколы проверки предметными комиссиями, которые после заполнения передаются в РЦОИ для дальнейшей обработки. В случае существенного расхождения в баллах, выставленных двумя экспертами, назначается третья проверка. Существенное расхождение в баллах определено в критериях оценивания по соответствующему учебному предмету.
Третий эксперт назначается председателем предметной комиссии из числа экспертов, ранее не проверявших экзаменационную работу.
Третьему эксперту предоставляется информация о баллах, выставленных экспертами, ранее проверявшими экзаменационную работу обучающегося. Баллы, выставленные третьим экспертом, являются окончательными.» (п. 48 Порядка ГИА-9).
«Полученные результаты в первичных баллах (сумма баллов за правильно выполненные задания экзаменационной работы) РЦОИ переводит в пятибалльную систему оценивания» (п. 52 Порядка ГИА-9).
«Результаты ГИА признаются удовлетворительными в случае, если обучающийся по обязательным учебным предметам набрал минимальное количество баллов, определенное органом исполнительной власти субъекта Российской Федерации, осуществляющим государственное управление в сфере образования, учредителем, загранучреждением» (п. 60 Порядка ГИА-9).
В дополнение к перечисленным выше требованиям Порядка определены следующие подходы к оценке экзаменационных работ по математике:
за каждое верно выполненное задание выставляется 1 первичный балл;
задание считается выполненным верно, если выпускник выбрал правильный путь решения, из письменной записи решения понятен ход его рассуждений, получен верный ответ;
если по результатам проверки экзаменационной работы двумя экспертами получены суммы, расходящиеся на два или более первичных баллов, то по заданиям, в которых обнаружены расхождения, назначается третья проверка; в других случаях расхождения оценки, выставленной двумя экспертами, окончательной считается более высокая оценка;
рекомендуется следующая шкала перевода суммы первичных баллов за выполненные задания ГВЭ-9 по математике в пятибалльную систему оценивания:
|
Отметка по пятибалльной системе оценивания |
«2» |
«3» |
«4» |
«5» |
|
Первичный балл |
0–2 |
3–6 |
7–8 |
9–10 |
Результаты государственной итоговой аттестации признаются удовлетворительными в случае, если выпускник при сдаче государственного выпускного экзамена по математике получил отметку не ниже удовлетворительной («три»).
1.2. Особенности экзаменационной работы ГВЭ-9 по математике (устная форма)
При разработке экзаменационной модели соблюдалась преемственность с традиционными устными экзаменами по математике для обучающихся по образовательным программам основного общего образования. Образец экзаменационного билета для проведения ГВЭ-9 по математике в устной форме представлен ниже.
На экзамене проверяется сформированность представлений выпускников о математике как универсальном языке науки, об идеях и методах математики, овладение математическими знаниями и умениями, соответствующими Федеральному компоненту государственного стандарта общего образования (Приказ Минобразования России от 05.03.2004 г. №1089), развитие логического мышления, пространственного воображения, алгоритмической культуры.
Для проведения ГВЭ-9 по математике в устной форме разработаны варианты билетов, включающие в себя задания как по курсу алгебры, так и по курсу геометрии. Билеты предназначены и для тех выпускников, которые осваивали программу в рамках двух предметов, и для тех, кто изучал математику в рамках интегрированного курса.
Билеты включают 5 заданий: теоретическая часть – два задания по геометрии, практическая часть – одно задание по арифметике и два задания по алгебре. Задания являются стандартными для курса математики основной школы. Все они предполагают устное изложение решения, демонстрирующего умение выпускника математически грамотно излагать ход решения, приводя при этом необходимые пояснения и обоснования.
Структура билета отвечает цели построения системы дифференцированного обучения в современной школе. Дифференциация обучения направлена на решение двух задач: формирования у всех учащихся базовой математической подготовки, составляющей функциональную основу общего образования, и создания для части школьников условий, способствующих получению подготовки более высокого уровня.
Задания в практической части экзаменационных билетах расположены по нарастанию сложности. Задания 3 и 4 соответствуют уровню базовой математической подготовки, среди них одно задание по арифметике и одно задание по алгебре. Задание 5 (по курсу алгебры) соответствуют уровню повышенной подготовки.
Теоретические вопросы билетов охватывают основные блоки содержания курса геометрии 7-9-х классов: «Признаки равенства треугольников», «Сумма углов треугольника», «Признаки подобия треугольников», «Свойства и признаки равнобедренного треугольника», «Свойства прямоугольных треугольников», «Свойства четырехугольников», что обеспечивает достаточную полноту проверки овладения содержанием курса (теоретические вопросы экзаменационных билетов даны в Приложении 2). Владение выпускниками материалом этих тем на уровне обязательной подготовки обеспечивает успешность обучения в старшей школе.
В первом вопросе экзаменационного билета от экзаменуемого требуется воспроизвести определение геометрической фигуры или конфигурации, формулировку теоремы, связанной с ее свойствами или признаками (доказывать теорему не требуется), привести необходимые иллюстрирующие примеры. Умение доказывать изученные в курсе свойства или признаки геометрических фигур, сформулированные в виде теорем, экзаменуемый должен продемонстрировать при ответе на второй вопрос билета. (Формулировки и доказательства, воспроизводимые экзаменуемым, могут различаться в зависимости от учебников, по которым экзаменуемый обучался и готовился к экзамену).
Ниже приводятся перечни теоретических вопросов экзаменационных билетов.
Первые вопросы экзаменационных билетов
1. Параллельные прямые; свойство углов, образованных при пересечении параллельных прямых секущей.
2. Равнобедренный треугольник; свойство углов при основании равнобедренного треугольника.
3. Высота, биссектриса и медиана треугольника; свойства медианы, биссектрисы, высоты равнобедренного треугольника, проведенных к основанию.
4. Признаки равенства треугольников.
5. Параллелограмм; свойства и признак параллелограмма.
6. Прямоугольник, квадрат, ромб; их свойства.
7. Трапеция; равнобедренная (равнобокая) трапеция; средняя линия трапеции и ее свойства.
8. Прямоугольный треугольник; свойство прямоугольного треугольника, один из углов которого равен 30.
9. Теорема синусов; пример ее применения для решения треугольников.
10. Теорема косинусов; пример ее применения для решения треугольников.
11. Теоремы о вписанной и описанной окружностях треугольника.
12. Косинус острого угла прямоугольного треугольника; пример его применения при решении прямоугольных треугольников.
13. Синус острого угла прямоугольного треугольника; пример его применения при решении прямоугольных треугольников.
14. Признаки подобия треугольников.
15. Окружность, градусная мера дуги окружности; центральный угол, вписанный угол; теорема о вписанном угле.
Вторые вопросы экзаменационных билетов
1. Признаки параллельности прямых (доказательство одного из признаков).
2. Свойства медианы, биссектрисы, высоты равнобедренного треугольника, проведённых к основанию (доказательство одного из свойств).
3. Теорема о сумме углов треугольника.
4. Теорема о средней линии трапеции.
5. Теорема Пифагора.
В соответствии со спецификой математики овладение теоретическими положениями курса алгебры проверяется опосредованно через проверку умения решать задачи. Задания, включенные в билеты, относятся к следующим разделам курса: «Числа и вычисления» (проценты; решение текстовых задач), «Функции», «Уравнения и неравенства». Все задания, используемые для составления экзаменационных вариантов, содержатся в открытом банке заданий ОГЭ.
Ниже приводится пример экзаменационного билета по математике.
Образец экзаменационного билета по математике
1. Признаки равенства треугольников (формулировки и пример применения одного из признаков).
2. Теорема Пифагора (формулировка и доказательство).
3. Дана система неравенств  На каком рисунке изображено множество решений этой системы?
На каком рисунке изображено множество решений этой системы?
|
1) система не имеет решений |
3)  |
|
2) 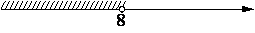 |
4) 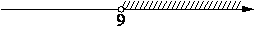 |
4. На диаграмме представлены некоторые из крупнейших по площади территории стран мира.

Во сколько примерно раз площадь США больше площади Судана? (Ответ округлите до целых.)
5. Решите уравнение x3 + 4x2 = 9x + 36.
При проверке математической подготовки выпускников оценивается уровень, на котором сформированы следующие умения:
воспроизводить определения геометрических объектов, формулировки теорем и их доказательства, сопровождая их необходимыми чертежами и рисунками;
использовать изученную математическую терминологию и символику;
приводить примеры геометрических фигур и конфигураций, примеры применения изученных свойств, фактов и методов;
отвечать на вопросы, связанные с изученными математическими фактами, понятиями и их свойствами, с методами решения задач;
четко, грамотно, логично излагать свои мысли;
выполнять арифметические действия, сочетая устные и письменные приемы;
вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования;
читать графики элементарных функций;
решать линейные и квадратные уравнения и неравенства, их системы.
При оценке экзаменационной работы используется пятибалльная шкала. Результаты государственной итоговой аттестации признаются удовлетворительными в случае, если выпускник при сдаче ОГЭ-9 по математике получил отметку не ниже удовлетворительной.
Оценивание результата экзамена по математике осуществляется в соответствии со следующими критериями.
|
Номер задания |
Критерии оценки выполнения задания |
Баллы |
|
№ 1 |
Ответ экзаменуемого характеризуется смысловой цельностью, речевой связностью и последовательностью изложения:
логические ошибки отсутствуют, последовательность изложения не нарушена;
Или:
допущена одна ошибка / неточность, которая после уточняющего вопроса экзаменатора исправлена экзаменуемым |
2 |
|
Ответ экзаменуемого характеризуется смысловой цельностью, связностью и последовательностью изложения,
но допущена одна ошибка / неточность, которую после уточняющего вопроса экзаменатора экзаменуемый не сумел исправить |
1 |
|
Другие случаи, не соответствующие указанным выше критериям |
0 |
|
№ 2 |
Ответ экзаменуемого характеризуется смысловой цельностью, речевой связностью и последовательностью изложения:
логические ошибки отсутствуют, последовательность изложения не нарушена;
Или:
допущена одна ошибка / неточность, которая после уточняющего вопроса экзаменатора исправлена экзаменуемым |
2 |
|
Ответ экзаменуемого характеризуется смысловой цельностью, связностью и последовательностью изложения,
но допущена одна ошибка / неточность, которую после уточняющего вопроса экзаменатора экзаменуемый не сумел исправить |
1 |
|
Другие случаи, не соответствующие указанным выше критериям |
0 |
|
№ 3 |
Дан полностью верный ответ: экзаменуемым выбраны все верные утверждения, неверные утверждения не выбраны |
2 |
|
Дан частично верный ответ: экзаменуемым выбраны не все верные утверждения или выбрано одно неверное утверждение |
1 |
|
Другие случаи, не соответствующие указанным выше критериям |
0 |
|
№ 4 |
Ход решения верный, получен верный ответ |
2 |
|
Ход решения верный, но экзаменуемый допустил одну ошибку вычислительного характера |
1 |
|
Другие случаи, не соответствующие указанным выше критериям |
0 |
|
№ 5 |
Ход решения верный, получен верный ответ |
2 |
|
Ход решения верный, но экзаменуемый допустил одну ошибку вычислительного характера |
1 |
|
Другие случаи, не соответствующие указанным выше критериям |
0 |
|
Максимальное количество баллов за экзаменационный билет |
10 |
Рекомендуется следующая шкала перевода суммы первичных баллов за выполненные задания ГВЭ-9 по математике (устная форма) в пятибалльную систему оценивания:
|
Отметка по пятибалльной системе оценивания |
«2» |
«3» |
«4» |
«5» |
|
Первичный балл |
0–3 |
4–6 |
7–8 |
9–10 |